Exponents: What Are They?

Sometimes, when we need to multiply a number many times, such as multiplying 2 by itself 100 times, writing each multiplication individually and performing the operation would not be practical. Instead, we use exponential notation to express such multiplications in a shorter form. Exponential expressions are shorthand for multiplying the same number repeatedly.

$a^n = a \times a \times a \times \dots \times a \quad (\text{n times})$

Additionally, the concept of a factorial works in a similar way. To represent the product of multiple numbers, we use factorial notation. For example, the product of all integers from 1 to (n) is written as (n!) (factorial). This is expressed as:

$n! = 1 \times 2 \times 3 \times \dots \times n$

This allows us to represent a large number of multiplications in a simplified form.

Exponential expressions and factorials are essential tools for efficiently writing and understanding mathematical operations.

Exponents provide a concise way to express repeated multiplication. A base number is multiplied by itself a specific number of times.

Example:
$5 \cdot 5 \cdot 5 \cdot 5 = 5^4$

General Information About Exponents

Positive Exponents

A positive exponent indicates how many times the base is multiplied by itself.

$a^n = a \cdot a \cdot a \cdot \cdots \quad \text{(n times)}$

Example:

$3^4 = 3 \cdot 3 \cdot 3 \cdot 3 = 81$

Negative Exponents

A negative exponent represents the reciprocal of the base raised to the corresponding positive power.

$a^{-n} = \frac{1}{a^n}, \quad \text{where } a \neq 0$

Example:

$2^{-3} = \frac{1}{2^3} = \frac{1}{8}, \quad 5^{-2} = \frac{1}{5^2} = \frac{1}{25}$

Zero Exponents

Any nonzero number raised to the power of zero equals 1:

$a^0 = 1, \quad \text{where } a \neq 0$

Examples:

$3^0 = 1, \quad (-7)^0 = 1$

Importance of Parentheses

Parentheses are critical when working with negative bases, as they determine how the exponent is applied:

$(-a)^n: \text{The exponent affects the entire negative base.}$

$-a^n: \text{The exponent applies only to the base, not the negative sign.}$

Examples:

$(-3)^2 = 9, \quad -3^2 = -(3^2) = -9$

$(-3)^3 = -27, \quad -3^3 = -(3^3) = -27$

Exponents represent how many times a number (the base) is multiplied by itself. For example:

$a^n = \underbrace{a \cdot a \cdot a \cdots}_{n \text{ times}}$

Exponential Numbers Operations

1. Addition and Subtraction

Exponents can only be added or subtracted if the bases and exponents are the same:

$a^n + a^n = 2a^n$

Example:

$3^2 + 3^2 = 2 \cdot 3^2 = 18$

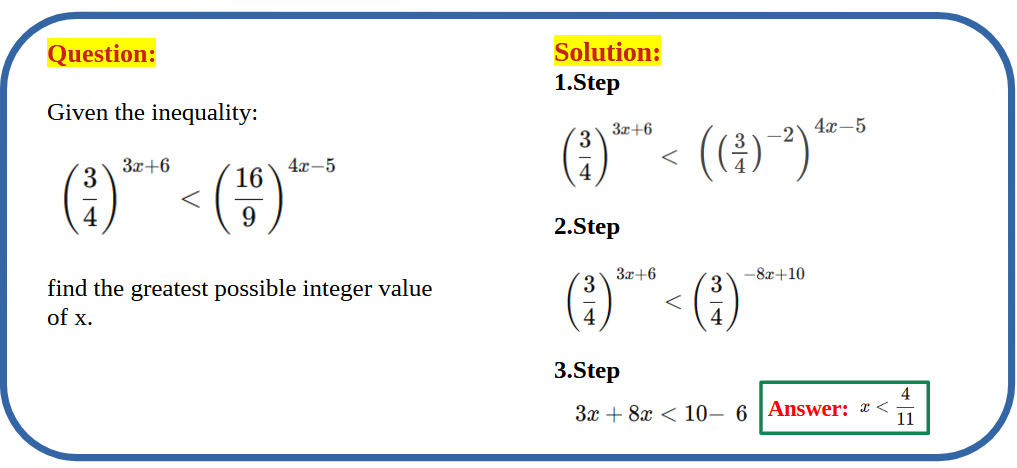
2. Multiplication

When multiplying exponents with the same base,add the powers:

$a^m \cdot a^n = a^{m+n}$

Example:

$2^3 \cdot 2^4 = 2^{3+4} = 2^7 = 128$

If the exponents are the same but the bases are different,multiply the bases:

$a^n \cdot b^n = (a \cdot b)^n$

Example:

$2^3 \cdot 3^3 = (2 \cdot 3)^3 = 6^3 = 216$

3. Division

When dividing exponents with the same base,subtract the powers:

$\frac{a^m}{a^n} = a^{m-n}$

Example:

$\frac{5^4}{5^2} = 5^{4-2} = 5^2 = 25$

If the exponents are the same but the bases are different,divide the bases:

$\frac{a^n}{b^n} = \left(\frac{a}{b}\right)^n$

Example:

$\frac{8^2}{4^2} = \left(\frac{8}{4}\right)^2 = 2^2 = 4$

4. Power of a Power

When raising an exponent to another power,multiply the exponents:

$\left(a^m\right)^n = a^{m \cdot n}$

Example:

$\left(3^2\right)^3 = 3^{2 \cdot 3} = 3^6 = 729$

Exponents: What Are They?

Example:

General Information About Exponents

Positive Exponents

Negative Exponents

Zero Exponents

Importance of Parentheses

Exponential Numbers Operations

1. Addition and Subtraction

2. Multiplication

3. Division

4. Power of a Power

Leave a Reply Cancel reply

Example:
$5 \cdot 5 \cdot 5 \cdot 5 = 5^4$