Rational Numbers
In mathematics, the term “ratio” refers to the comparison of the sizes of two different quantities. For example, if there are three women for every one man in a class, the ratio of men to women is 1 to 3. Ratios are often written as fractions. In this example, the ratio of men to women is expressed as 1/3. Therefore, numbers that can be written as fractions are called rational numbers.
Rational Numbers and Fractions
A rational number is any number that can be written as a fraction in the following form:
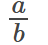
- a is the numerator, which is an integer.
- b is the denominator, which is also an integer (but b cannot be zero).
A rational number can be located on a number line; most rational numbers lie between whole numbers.
Irrational Numbers
Irrational numbers are numbers that cannot be expressed as a fraction (a/b). Their decimal representation goes on forever and never repeats.
- π (Pi) ≈ 3.14159…
- √2 (Square root of 2) ≈ 1.41421…
- e (Euler’s number) ≈ 2.71828…

Proper Fraction:
A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). Proper fractions represent values less than 1.
Example:
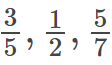
Improper Fraction:
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Improper fractions represent values greater than or equal to 1.
Example:


Mixed Fraction:
A mixed fraction is a combination of a whole number and a proper fraction. This is usually used to express an improper fraction in a more readable form.
Example:
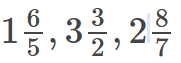

Absolute Value of Fractions
Signs of Fractions
Fractions can be thought of as the division of two integers. The following rules apply to signed fractions:
- Negative Fractions:
If either the numerator or denominator is negative, the fraction becomes negative.
Example: -2/3 or 2 /-3 is a negative fraction.
- Writing the Negative Sign of a Fraction:
To indicate a negative sign, we can either make the numerator or denominator negative, or place the negative sign in front of the fraction.
Example: -2/3 and 2/-3 are equivalent.

